国庆版本明日更新！算算勋章强化的期望及复杂计算过程？

今天就是春节版本的更新了，随意算了算勋章加强的期望。

110版本增速

勋章加强的本质为安全加强，安全加强的估算过程比普通加强要复杂得多，由于存在机率补正。

若果依照基本算法，以4上5为例：

设第1次的成功率p1，第n次的成功率为pn，单次成本为c，最多须要加强6次

则1次成功发生的机率为p1，2次成功发生的机率为(1-p1)p2，3次成功发生的机率为(1-p1)(1-p2)p3，4次成功发生的机率为(1-p1)(1-p2)(1-p3)p4，5次成功发生的机率为(1-p1)(1-p2)(1-p3)(1-p4)p5，6次成功发生的机率为(1-p1)(1-p2)(1-p3)(1-p4)(1-p5)

所以4上5的平均成本为f=p1*c+(1-p1)p2*2c+(1-p1)(1-p2)p3*3c+(1-p1)(1-p2)(1-p3)p4*4c+(1-p1)(1-p2)(1-p3)(1-p4)p5*5c+(1-p1)(1-p2)(1-p3)(1-p4)(1-p5)6c

根据这个算法，在加强10以上时补正只有0.01，最多可以失败90次，算法将会异常庞大，所以要对算法进行改进。

由于每次加强的成本都是一样的，所以只须要算出加强的平均次数t即可

无论成功与否，第1次加强都是必然发生的，所以第1次加强发生的机率为t1=1

只要第1次加强失败，第2次加强就必然发生，所以第2次加强发生的机率为t2=1-p1

只要第2次加强失败，第3次加强就必然发生，所以第3次加强发生的机率为t3=(1-p1)(1-p2)

只要第3次加强失败，第4次加强就必然发生，所以第4次加强发生的机率为t4=(1-p1)(1-p2)(1-p3)

只要第4次加强失败，第5次加强就必然发生，所以第5次加强发生的机率为t5=(1-p1)(1-p2)(1-p3)(1-p4)

只要第5次加强失败，第6次加强就必然发生，所以第6次加强发生的机率为t6=(1-p1)(1-p2)(1-p3)(1-p4)(1-p5)

由此可以算出加强的平均成本f=c*t=c(t1+t2+t3+t4+t5+t6)=c(1-p1+(1-p1)(1-p2)+(1-p1)(1-p2)(1-p3)+(1-p1)(1-p2)(1-p3)(1-p4)+(1-p1)(1-p2)(1-p3)(1-p4)(1-p5))

假如你有一定的物理基础，会发觉这个公式上个公式似乎是同一个公式。

但这个公式除了愈发简练，但是收敛速率更快，更容易求出近似值。

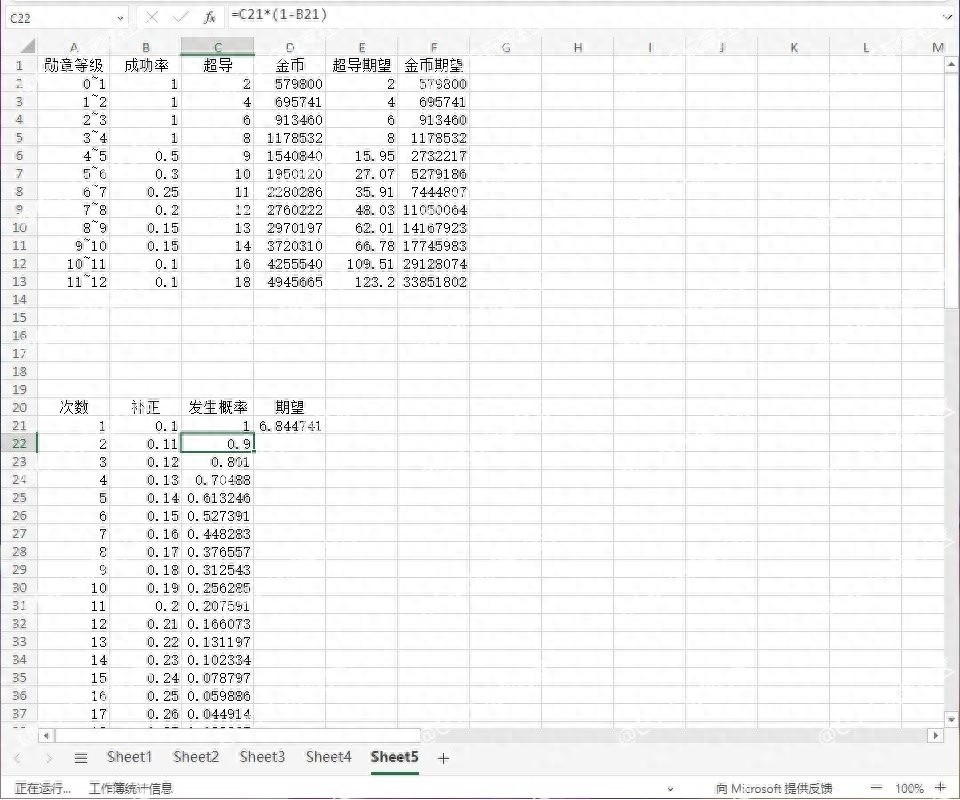
接出来就是无趣的估算了，4上5耗费的平均次数为t=1-0.5+(1-0.5)(1-0.6)+(1-0.5)(1-0.6)(1-0.7)+(1-0.5)(1-0.6)(1-0.7)(1-0.8)+(1-0.5)(1-0.6)(1-0.7)(1-0.8)(1-0.9))=1.7732，即9*1.7732=15.95个材料，1540840*1.7732=2732217金币

5上6耗费的平均次数为2.7071，即27.07个材料，5279186金币

6上7耗费的平均次数为3.2648，即35.91个材料，7444807金币

7上8耗费的平均次数为4.0033，即48.03个材料，11050064金币

8上9耗费的平均次数为4.7700，即62.01个材料，14167923金币

9上10耗费的平均次数为4.7700，即66.78个材料，17745983金币

10上11耗费的平均次数为6.8447，即109.51个材料，29128074金币

11上12耗费的平均次数为6.8447，即123.2个材料，33851802金币